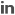DISTINCT ENERGIES OF CHOLESTEROL
HTML Full TextDISTINCT ENERGIES OF CHOLESTEROL
M. R. Rajesh Kanna*1, 2, D. Soner Nandappa 3 and R. Pradeep Kumar 3
Department of Mathematics 1, Maharani's Science College for Women, J. L. B. Road, Mysore - 570005, Karnataka, India.
Department of Mathematics 2, Government First Grade College, Bettampady, Puttur, Dakshina, Kannada - 574259, Karnataka, India.
Department of Studies in Mathematics 3, University of Mysore, Mysuru - 570006, Karnataka, India.
ABSTRACT: Cholesterol is a waxy substance which is made in the body by the liver but is also found in some foods. It plays a vital role in how every cell works and is also needed to make Vitamin D, some hormones and bile for digestion. The concept of energy of a graph was introduced by I. Gutman in the year 1978. In this paper, we compute Siedel Energy, Maximum Degree Energy, Distance Energy, Harary Energy of Cholesterol.
| Keywords: |
Eigen values, Siedel energy, Maximum degree energy, Distance energy, Harary energy, Cholesterol
INTRODUCTION: Cholesterol is a lipid with a unique structure consisting of four linked hydrocarbon rings forming the bulky steroid structure. There is a hydrocarbon tail linked to one end of the steroid and a hydroxyl group linked to the other end. The hydroxyl group is able to form hydrogen bonds with nearby carbonyl oxygen of phosphor lipid and sphingolipid head groups. Cholesterol is known as a sterol because it is made out of an alcohol and steroid. Cholesterol is present in most animal membranes with varying amounts but is absent in prokaryotes and intracellular membranes. Cholesterol is one of the basic sterols which occurs in all animal tissues and is of great importance to animal life.
The thermodynamic properties of this material are, therefore, important in the study of the biochemical processes in which it is involved. It is one of the biomedical chemicals which is certified for purity and ordered as a standard reference material (SRM 9Ila) by the NBS Office of Standard Reference Materials. Since this material is of natural origin it is expected to be essentially free of sterol isomers.
FIG. 1: STRUCTURE OF CHOLESTEROL
In 1927, Wieland and Adolf Windaus got Nobel Prize for cholesterol and bile acids structure. In 1932, Adolf Windaus clarified the structure of cholesterol. In 1964, Dr. Konrad Bloch received the Nobel Prize for explaining the cholesterol synthesis. He showed HMG-CoA reductase was the enzyme in this complex synthesis. The cholesterol serves as a precursor for bile acids, sex hormones, and cortisol. Konrad Bloch and Feodor Lynen awarded Nobel Prize for cholesterol and fatty acids metabolism.
Cholesterol is a waxy substance which is made in the body by the liver but is also found in some foods. It plays a vital role in how every cell works and is also needed to make Vitamin D, some hormones and bile for digestion. Cholesterol is both our friend and foe - at normal levels, it is an essential substance for the body's normal functioning, but if levels in the blood get too high, it becomes a silent danger that puts us at risk of a heart attack.
Cholesterol is carried in the blood attached to proteins called lipoproteins. There are two main forms, LDL (low density lipoprotein) and HDL (high density lipoprotein). LDL cholesterol is often referred to as bad cholesterol" because too much is unhealthy. HDL is often referred to as good cholesterol because it is protective. Knowing the levels of these can help us to determine the risk of heart disease.
Molecules and molecular compounds are often modeled by molecular graph. A molecular graph is a representation of the structural formula of chemical compound in terms of graph theory, whose vertices correspond to the atoms of the compound and edges correspond to chemical bonds. Note that hydrogen atoms are often omitted. All molecular graphs considered in this paper are finite, connected, loop less, and without multiple edges. Let G = (V, E) be a graph with vertex set V and edge set E. The degree of a vertex u є E is denoted by du and is the number of vertices that are adjacent to u. The edge connecting the vertices u and v is denoted by uv.
Let be a simple graph of order n with vertex set V = {v1, v2 ...., vn} and edge set E.
The concept of energy of a graph was introduced by I. Gutman 1 in the year 1978.
Definition 1: The adjacency matrix of G is the n × n matrix defined by A (G) = (aij), where

The Eigen values λ1, λ2 . . . λn of A (G), assumed in none increasing order, are the Eigen values of the graph G. As A is real symmetric, the Eigen values of G are real with sum equal to zero. The energy E (G) of G is defined to be the sum of the absolute values of the Eigen values of G i.e.
![]()
For details on the mathematical aspects of the theory of graph energy see the reviews 2, papers 3-5 and the references cited there in. The basic properties including various upper and lower bounds for energy of a graph have been established in 6-7, and it has found remarkable chemical applications in the molecular orbital theory of conjugated molecules 8-9. Recently authors of this paper computed energy of Cholesterol 10.
In chemistry, the Eigen values represent the energy levels of the electrons in a molecule. The total π-electron energy E is the sum of the energies of all electrons in a molecule. The π-electron energy of a conjugated carbon molecule, computed using the Huckel theory, coincides with the energy as defined here. Hence results on graph energy assume special significance.
RESULTS AND DISCUSSIONS:
Siedel Energy: Let G be a simple graph of order n with vertex set V = {v1, v2 ...., vn} and edge set E.
Definition 2: The Siedel matrix of G is the n × n matrix denoted by S (G):=(sij), where

The characteristic polynomial of S (G) is denoted by fn(G, λ) = det(λI – S(G)). The Seidel Eigen values of the graph G are the Eigen values of S (G). Since S (G) is real and symmetric, its Eigen values are real numbers. The Seidel energy 11 of G defined as
![]()
Theorem 1: The Seidel energy of cholesterol C27H46O is 92.4048.
Proof: Consider a molecular graph of cholesterol C27H46O as shown in the following figure. Here vertices are numbered from 1 to 27.
Siedel matrix S C27H46O =

Seidel Eigen values are - 5.7653, -5.3085, -4.7155, -4.3272, -4.1246, -3.6630, -3.5870, -2.9693, 2.8077, -2.2836, -1.7611, -1.4999, -1.0000, -1.0000, -0.8582, -0.5314, 0.2864, 0.7493, 1.1671, 1.3602, 1.8557, 2.1002, 2.3920, 2.7396, 3.1094, 3.6053, 4.1364, 22.7008.
Seidel energy of a cholesterol is SE C27H46O = |-5.7653| + |-5.3085| + |-4.7155| + |-4.3272| + |4.1246| + |-3.6630| + |-3.5870| + |-2.9693| + |-
2.8077| + |-2.2836| + |-1.7611| + |-1.4999| + |-1.0000| + |-1.0000| + |-0.8582| + |-0.5314| + |0.2864| + |0.7493| + |1.1671| + |1.3602| + |1.8557| + |2.1002| + |2.3920| + |2.7396| + |3.1094| + |3.6053| + |4.1364| + |22.7008| = 92.4048
Maximum Degree Energy: C. Adiga and M. Smitha 12 defined maximum degree energy of a graph. Let G be a simple graph of order n with vertex set V = {v1, v2 ...., vn} and edge set E.
Definition 3: The maximum degree matrix of G is the n × n matrix defined by AMD (G):= (aij), where

The characteristic polynomial of by AMD (G) is denoted by fn(G, λ) = det(λI – S(G)). The maximum degree Eigen values of the graph G are the Eigen values of AMD (G). Since AMD (G) is real and symmetric, its Eigen values are real numbers and we label them in non-increasing order λ1 ≥ λ2 ≥ ... ≥ λn. The maximum degree energy of defined as
![]()
Theorem 2: The maximum degree energy of cholesterol C27H46O is 105.9520.
Proof: The maximum degree matrix of cholesterol is AMD C27H46O =

Maximum degree Eigen values are -9.0371, -8.4868, -5.8588, -5.4042, -5.2821, -4.4786, -3.8268, -3.4847, -2.6850, -2.0074, -1.4005, -0.7548, -0.2692, -0.0000, 0.0000, 0.3403, 0.9849, 1.5335, 2.0806, 2.4522, 3.3577, 3.8326, 4.4780, 5.1679, 5.4000, 5.6746, 8.5682, 9.1054.
Maximum degree energy of a cholesterol is EMD (C27H46O) |-9.0371| + |-8.4868| + |-5.8588| + |-5.4042| + |-5.2821| + |-4.4786| + |-3.8268| + | -3.4847| + |-2.6850| + |-2.0074| + |-1.4005| +|-
0.7548| + | -0.2692| + |-0.0000| + |0.0000| + |0.3403| + |0.9849| + |1.5335| + |2.0806| + |2.4522| + |3.3577| + |3.8326| + |4.4780| + |5.1679| + |5.4000| + |5.6746| + |8.5682| + |9.1054| = 105.9520.
Distance Energy: Gopalapillai Indulal et al., 13 defined distance energy of graphs. Let G be a simple graph of order n with vertex set V = {v1, v2 ...., vn} and edge set E.
Definition 4: The distance matrix of G is the square matrix of order n whose (i, j) entry is the shortest distance between the vertices vi and vj. Let λ1, λ2, . . . ,λn be the Eigen values of the distance matrix of G. The distance energy DE is defined as
![]()
Theorem 3: The distance energy of cholesterol C27H46O is 328.3176.
Proof: The distance matrix of cholesterol is D C27H46O =

Distance Eigen values are -72.7700, -29.6860, -13.6556, -9.3113, -7.4864, -5.7116, -5.0599, -3.1580, -3.0693, -2.6724, -2.0821, -1.8804, -1.4986, -1.2677, -1.1933, -1.0229, -0.7876, -0.7063, -0.5414, -0.5001, -0.0978, -0.0000, 0.0880, 0.1681, 0.4935, 0.8872, 12.2914, 150.2307.
Distance energy of a cholesterol is DE C27H46O = |-72.7700 | + | -29.6860| + |-13.6556| + |-9.3113| + |-7.4864| + |-5.7116| + |-5.0599| + |-3.1580| + |-3.0693| + |-2.6724| + |-2.0821| + |-1.8804| + |-1.4986| + |-1.2677| + |-1.1933| + |-1.0229| + |-0.7876| + |-0.7063| + |-0.5414| + |-0.5001| + |-0.0978| + |-0.0000| + |0.0880| + |0.1681| + |0.4935|+ |0.8872| + |12.2914| + |150.2307| = 328.3176.
Harary Energy: The concept of Harary was introduced by A. Dilek Güngör and A. Sinan Çevik
- 14. Let G be a simple graph of order n with vertex set V = {v1, v2 ...., vn} and edge set E.
Definition 5: The Harary matrix of G is the square matrix of order n whose (i, j) entry is 1/dij where dij is the distance between the vertices vi and vj. Let λ1, λ2. . . λn be the Eigen values of the Harary matrix of G. The Harary energy, HE (G) is defined by
![]()
Further studies on Harary energy can be found in15.
Theorem 4: The Harary energy of cholesterol C27H46O is 36.5093.
Proof: The Harary matrix of cholesterol is H (C27H46O) =

Harary Eigen values are -1.8471, -1.5175, -1.5014, -1.4253, -1.3437, -1.3132, -1.2673, -1.2141, -1.1722, -1.0569, -1.0071, -0.7066, -0.6466, -0.6106, -0.5231, -0.4968, -0.3526, -0.2341, -0.0184, 0.0336, 0.2585, 0.4867, 0.9153, 0.9361, 1.2310, 2.5362, 3.4653, 8.3920.
Harary energy of a cholesterol is HE (C27H46O) = |-1.8471| + |-1.5175| + |-1.5014| + |-1.4253| + |-1.3437| + |-1.3132| + |-1.2673| + |-1.2141| + |-1.1722| + |-1.0569| + |-1.0071| + |-0.7066| + |-0.6466| + |-0.6106| + |-0.5231| + |-0.4968| + |-0.3526| + |-0.2341| + |-0.0184| + |0.0336| + |0.2585| + |0.4867| + |0.9153| + |0.9361| + |1.2310| + |2.5362| + |3.4653| + |8.3920| = 36.5093.
CONCLUSION: In this paper, we compute Siedel energy, Maximum degree energy, Distance energy, Harary energy of cholesterol.
ACKNOWLEDGEMENT: The authors are thankful to the reviewers for their valuable suggestions.
CONFLICT OF INTERESTS: The authors declare that there is no conflict of interests regarding the publication of this paper.
REFERENCES:
- Gutman I: The energy of a graph. Ber. Math-Statist. Sekt. Forschungsz. Graz 1978; 103: 1-22.
- Gutman I, Betten A, Kohnert R and Laue A: The energy of a graph: Old and New Results, ed. by Wassermann. Algebraic Combinatorics and Applications (Springer, Berlin, 2001; 196 - 211.
- Cvetković D and Gutman I: Applications of Graph Spectra Mathematical Institution, Belgrade 2009.
- Cvetković D and Gutman I: Selected Topics on Applications of Graph spectra, Mathematical Institute Belgrade 2011.
- Gutman I, Li X and Zhang J: in Graph Energy, Analysis of Complex Networks. From Biology to Linguistics. Wiley - VCH, Weinheim 2009; 145 - 174
- Liu H, Lu M and Tian F: Some upper bounds for the energy of graphs Journal of Mathematical Chemistry 2007; 41(1).
- McClelland BJ: Properties of the latent roots of a matrix: The estimation of π-electron energies. J. Chem. Phys. 1971; 54: 640 - 643.
- Graovać A, Gutman I and Trinajstic N: Topological Approach to the Chemistry of Conjugated Molecules. Springer, Berlin 1977.
- Gutman I and Polansky OE: Mathematical Concepts in Organic Chemistry. Springer, Berlin 1986.
- Kanna MRR and Kumar RP: Computation of Energy of Cholesterol, Asian Academic Research Journal of Multidisciplinary 3(10): 255-259.
- Willem HH: Seidel Switching and Graph Energy, MATH Commun. Math. Comput. Chem, 2012; 68: 653-659.
- Adiga C and Smitha M: On maximum degree energy of a graph. Int. J. Contemp. Math. Sciences 2009; 4(8): 385 - 396.
- Indulal G, Gutman I and Kumar VA: On Distance Energy of Graphs, MATCH Commun. Comput. Chem. 2008; 60: 461-472.
- Güngör AD and Çevik AS: On the Harary Energy and Harary Estrada Index of a Graph MATCH Commun. Math. Comput. Chem. 2010; 64: 281-296.
- Cui Z and Liu B: On Harary Matrix, Harary Index and Harary Energy, MATCH Commun. Math. Comput. Chem. 2012; 68: 815-823.
How to cite this article:
Kanna MRR, Nandappa DS and Kumar RP: Distinct energies of cholesterol. Int J Pharm Sci Res 2017; 8(6): 2612-18.doi: 10.13040/ IJPSR.0975-8232.8(6).2612-18.
All © 2013 are reserved by International Journal of Pharmaceutical Sciences and Research. This Journal licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
Article Information
35
2612-2618
424
1498
English
IJPSR
M. R. Rajesh Kanna*, D. Soner Nandappa and R. Pradeep Kumar
Department of Mathematics, Maharani's Science College for Women, Mysore, Karnataka, India
mr.rajeshkanna@gmail.com
18 June, 2016
28 August, 2016
17 September, 2016
10.13040/IJPSR.0975-8232.8(6).2612-18
01 December, 2016