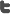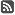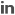ON SOME TOPOLOGICAL INDICES OF TRIANGULAR SILICATE AND TRIANGULAR OXIDE NETWORKS

ON SOME TOPOLOGICAL INDICES OF TRIANGULAR SILICATE AND TRIANGULAR OXIDE NETWORKS

Fazal Dayan ^*1, Bilal Ahmad ², Muhammad Zulqarnain ¹, Umar Ali ¹, Yasir Ahmad ³ and Tariq Javed Zia ⁴

Department of Mathematics ¹, School of Science, University of Management and Technology, Lahore, Pakistan.

Department of Mathematics ², The University of Lahore, Lahore, Pakistan.

Department of Mathematics ³, Comsat Institute of Information Technology, Lahore, Pakistan.

Department of Mathematics ⁴, Comsat Institute of Information Technology Islamabad, Pakistan.

ABSTRACT: A topological index is a numeric quantity from the structural graph of a molecule. It has become a very useful tool in the prediction of pharmacological, toxicological and physico - chemical properties of a compound. In this paper, we have computed some topological indices of triangular silicate TsL (n) and triangular oxide TOL (n) networks.

Topological index, Triangular oxide network, Triangular silicate network, Harrary index, Wiener index, Forgotten index

INTRODUCTION: Let G be a simple connected graph with n vertices and m edges. A simple graph is a molecular graph if its vertices and edges correspond to atoms and bonds respectively. A simple graph is an undirected and un-weighted graph with no multiple edges or loops. If there is a path between all pairs of vertices in a graph, then the graph is called a connected graph. So a molecular graph is always a simple connected graph. Graph theory has found considerable use in modeling chemical structures. Chemical graph theory is an important branch of mathematical chemistry that uses graph theory in the mathe-matical modeling of chemical phenomena ^{1, 2, 3}.

Chemical graph theory has an important effect in the development of mathematical chemistry and chemical sciences. Computing topological indices in mathematical chemistry is an important branch.

Topological index has become a very useful tool in the prediction of physiochemical and pharma-cological properties of a compound. The number of vertices and edges are the topological index molecular structure matters. The main ingredients of the molecular topological models are topological indices which are the topological characterization of molecules by means of numerical invariants. These models are instrumental in the discovery of new applications of molecules with specific chemical, pharmacological and biological properties. Applications of graph theory have led to the emergence of a number of graph-theoretical indices ⁴. These indices are used by various researchers in their studies. The first use of a topological index was made by the chemist Harold Wiener ⁵ in 1947.

In recent years many researchers have worked on computing topological indices ^{6, 7, 8, 9, 10, 11, 12, 13, 14}. Bharati R et al., have calculated the Zagreb, Randić and ABC index of silicate, honeycomb and hexagonal networks ¹⁵.

Kulli introduced the first and second K-Banhatti indices of a graph in ¹⁶. Kulli also defined some properties of these newly defined indices. The coindices of K-Banhatti indices were also defined in his work. Later kulli defined K hyper-Banhatti indices of V-Phenylenic nanotubes and nanotorus ¹⁷. Gutman et al., developed relations between Banhatti and Zagreb indices and discussed the lower and upper bounds for Banhatti indices of a connected graph in terms of Zagreb indices ¹⁸. Kulli et al also computed Banhatti indices for certain families of benzenoid systems ¹⁹. Moreover, Kulli introduced multiplicative hyper-Banhatti indices and coindices, Banhatti geometric-arithmetic index connectivity Banhatti indices for certain families of benzenoid systems ^20-21. Fazal Dayan et al., ²² computed Banhatti indices for triangular silicate, triangular oxide, rhombus silicate and rhombus oxide networks. Fazal Dayan et al., ²³ also computed Banhatti indices for hexagonal, honeycomb and derived networks.

In recent years many researchers have worked on computing topological indices ^24-26.

In this study, we compute some topological indices of TsL (n) and TOL (n) networks. Silicates are the largest, the most complicated and the most interesting class of minerals by far. SiO₄ tetrahedron is the basic chemical unit of silicates. The silicates sheets are rings of tetrahedrons linked by shared oxygen nodes to other rings in two dimensional planes producing a sheet like structures. A silicate can be obtained by fusing a metal oxide or a metal carbonate with sand. Essentially every silicate contains SiO₄ tetrahedron.

The corner and the center vertices represent oxygen and silicon ions respectively. These vertices are called oxygen nodes and silicon node respectively. A Silicate network is obtained in different ways. Paul Manuel has constructed a silicate network from a honeycomb network ⁵. In Fig. 1, SiO₄ tetrahedra is shown where the corner and the center vertices represent oxygen and silicon ions respectively.

In Fig. 2 and 3, triangular silicate network of order 3 and 4 are given.

Following are the types of edges based on the degree of the vertices of each edge in a triangular silicate network from level 4. These six types are given in the Table 1.

TABLE 1: TYPES AND NUMBER OF EDGES IN A TRIANGULAR SILICATE NETWORK

	(3, 3)	(3, 7)	(7, 12)	(12, 12)	(7, 7)	(3, 12)
Total number of edges	3	33+9 (n-4)	12+6 (n-4)		3(n-1)

Following are the four types of edges based on the degree of the vertices of each edge in a triangular

oxide network from level 4. These four types are given in the Table 2.

TABLE 2: TYPES AND NUMBER OF EDGES IN A TRIANGULAR OXIDE NETWORK

	(2, 4)	(4, 4)	(4, 6)	(6, 6)
Total number of edges	6	3(n-1)	6(n-2)

Harrary Index, Wiener Index and Forgotten Index: For a simple graph G, the Harrary, Wiener and Forgotten indices are given by:

Where du and dv denote the degree of the vertex u and v in G respectively.

Main Results:

Theorem: For a triangular silicate network, TsL (n) of dimension n, the Harrary index is given by

Proof:

Theorem: For a triangular oxide network, TOL (n) of dimension n, the Harrary index is given by

Proof:

Theorem: For a triangular silicate network, TsL (n) of dimension, the Wiener index is given by

Proof:

Theorem: For a triangular oxide network, ToL (n) of dimension n, the Wiener index is given by

Proof:

Theorem: For a triangular silicate network, TsL(n) of dimension n, the Forgotten index is given by

Proof:

Theorem: For a triangular oxide network, ToL(n) of dimension n, the Forgotten index is given by

Proof:

CONCLUSION: In this paper, we have computed some topological indices i.e. the Harrary Index, the Wiener Index and the Forgotten Index for triangular silicate network and triangular oxide network that will help to understand the physical features, chemical reactivities and biological activities of the triangular silicate and triangular oxide networks. These results can also provide a significant determination in the pharmaceutical industry.

ACKNOWLEDGEMENT: The authors are very grateful to the editor and reviewers for their comments and suggestions, which are helpful in improving the paper.

CONFLICT OF INTEREST: Nil

REFERENCES:

1. Gutman I and Trinajstic N: Graph theory and Molecular orbitals. Total electron energy of alternate hydrocarbons, Chem. Phys. Lett. 1972; 17: 535-538.
2. Randic M: J. Amer. Chem. Soc. 1975; 97: 6609.
3. Klarner DA: Polyominoes, In: Goodman JE and Rourke JO: Hand book of Discrete and Computational Geometry. CRC Press, Boca Raton. Chapter 1997; 12: 225-242.
4. Alaeiyan M, Bahrami A and Yazdani J: Schultz Index of Nanoporous, Australian Journal of Basic and Applied Sciences 2011; 5(6): 250-252.
5. Wiener H: Structural determination of paraffin boiling points. J. Am. Chem. Soc. 1947; 69: 17-20.
6. Gutman I: Degree-Based topological indices. Croat. Chem. Acta 2013; 86: 315-361.
7. Garcia I, Fall Y and Gomez G: Using topological indices to predict anti - alzheimer and anti - parasitic GSK-3 inhibitors by multi-target QSAR in-silico Molecules 2010; 15: 5408-5422.
8. Furtula B, Gutman I and Dehmer M: On structure-sensitivity of degree based topological indices. Appl. Math. Comput. 2013; 219: 8973-8978.
9. Hao J: Theorems about zagreb indices and modified zagreb indices. Match Commun. Math. Comput. Chem. 2011; 65: 659-670.
10. Xu K, Liu M, Das KC, Gutman I and Furtula B: A survey on graphs extremely with respect to distance-based topological indices. Match Commun. Math. Comput. Chem 2014; 71: 461-508.
11. Klavzar S and Deutsch E: M-Polynomial and Degree-Based Topological Indices. Iran. J. Math. Chem. 2015; 6: 93-102.
12. Dobrynin AA, Entringer R and Gutman I: Wiener index of trees: Theory and applications. Acta Appl. Math 2001; 66: 211-249.
13. Kier LB and Hall LH: Molecular Connectivity in Structure - Activity Analysis; John Wiley and Sons: NY, USA 1986.
14. Zhong L: The harmonic index for graphs. Appl. Math. Lett. 2012; 25: 561-566.
15. Rajan B and William A: Cyriac Grigorious and Sudeep Stephen, on certain topological indices of silicate, honey-comb and hexagonal networks, J. Comp. and Math. Sci. 2012; 3(5): 530-535.
16. Kulli VR: K-Banhatti indices of graphs, Journal of Computer and Mathematical Sciences 2016; 7(4): 213-218.
17. Kulli VR: On K Banhatti indices and K hyper-Banhatti indices of V-Phenylenic nanotubes and nanotorus, Journal of Computer and Mathematical Sciences 2016; 7(6): 302-307.
18. Gutman, Kulli VR, Chaluvaraju B and Baregowda HS: On Banhatti and Zagreb indices, Journal of the International Mathematical Virtual Institute 2017; 7: 53-67.
19. Kulli VR, Chaluvaraju B and Boregowda HS: Connectivity Banhatti indices for certain families of benzenoid systems. Journal of Ultra Chemistry 2017; 13(4): 81-87.
20. Kulli VR: Multiplicative hyper-Banhatti indices and coindices of graphs. International Journal of Mathematical Archive 2016; 7(6): 60-65.
21. Kulli VR: A new Banhatti geometric-arithmetic index, International Journal of Mathematical Archive 2017; 8(4): 112-115.
22. Dayan F, Javaid M, Ali U, Ahmad B and Zulqarnain M: On some banhatti indices of triangular silicate, triangular oxide, rhombus silicate and rhombus oxide networks. American Journal of Information Science and Technology 2018; 2(2): 42-49. doi: 10.11648/j.ajist. 20180202.13
23. Dayan F, Javaid M, Zulqarnain M, Ali MT and Ahmad B: Computing banhatti indices of hexagonal, honeycomb and derived networks. American Journal of Mathematical and Computer Modelling 2018; 3(2): 38-45. doi: 10.11648/ j.ajmcm.20180302.11
24. Klavzar S and Deutsch E: M-Polynomial and Degree-Based Topological Indices. Iran. J Math Chem 2015; 6: 93-102.
25. Kulli VR: Computing banhatti indices of networks, Int Journal of Advances in Mathematics 2018; 1: 31-40.
26. Zhong L: The harmonic index for graphs. Appl. Math. Lett 2012; 25: 561-566.
    

    ---

    How to cite this article:

    Dayan F, Ahmad B, Zulqarnain M, Ali U, Ahmad Y and Zia TJ: On some topological indices of triangular silicate and triangular oxide networks. Int J Pharm Sci & Res 2018; 9(10): 4326-31. doi: 10.13040/IJPSR.0975-8232.9(10).4326-31.

    ---

    All © 2013 are reserved by International Journal of Pharmaceutical Sciences and Research. This Journal licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.

    ---